Gnu octave version 4.0
Содержание:
- Стартовые файлы[править]
- Завершение работы Octaveправить
- Приложения с графическим интерфейсом
- [править] Переменные
- Entering commands[edit | edit source]
- How do I install or load all Octave Forge packages?[edit]
- Простые примеры
- использованная литература
- How do I change color/line definition in gnuplot postscript?[edit]
- Что-же дальше?
- High-Level Overview
- Создание матрицы[править]
- Why is Octave’s floating-point computation wrong?[edit]
- Пример[править]
- Октава, язык
- Совместимость с MATLAB
- [править] Служебные символы
- Troubleshooting
Стартовые файлы[править]
При запуске Octave, производится поиск команд для выполнения из файлов, перечисленных ниже. Эти файлы могут содержать любые команды Octave, включая определения функций.
| Файл | Описание |
|---|---|
| octave-home/share/octave/site/m/startup/octaverc | Where octave-home is the directory in which all of Octave is installed (the default is /usr/local/octave/cvs). This file is provided so that changes to the default Octave environment can be made globally for all users at your site for all versions of Octave you have installed. Some care should be taken when making changes to this file, since all users of Octave at your site will be affected. |
| octave-home/share/octave/version/m/startup/octaverc | Where octave-home is the directory in which all of Octave is installed (the default is /usr/local/octave/cvs), and version is the version number of Octave. This file is provided so that changes to the default Octave environment can be made globally for all users for a particular version of Octave. Some care should be taken when making changes to this file, since all users of Octave at your site will be affected. |
| ~/.octaverc | This file is normally used to make personal changes to the default Octave environment. |
| .octaverc | This file can be used to make changes to the default Octave environment for a particular project. Octave searches for this file in the current directory after it reads ~/.octaverc. Any use of the cd command in the ~/.octaverc file will affect the directory that Octave searches for the file .octaverc.
If you start Octave in your home directory, commands from from the file ~/.octaverc will only be executed once. |
A message will be displayed as each of the startup files is read if you invoke Octave with the —verbose option but without the —silent option.
Завершение работы Octaveправить
— Встроенная функция: exit (status)— Встроенная функция: quit (status)
- Exit the current Octave session. If the optional integer value status is supplied, pass that value to the operating system as the Octave’s exit status. The default value is zero.
— Встроенная функция: atexit (fcn)
- Register a function to be called when Octave exits. For example this code will print the message «Bye bye» when Octave exits.
functionbye_bye ()
disp("Bye bye");
endfunction
atexit("bye_bye");
— Встроенная функция: atexit (fcn, flag)
- Register or unregister a function to be called when Octave exits, depending on flag. If flag is true, the function is registered, if flag is false, it is unregistered. For example, after registering the function bye_bye as above,
atexit("bye_bye",false);
- will remove the function from the list and Octave will not call the function bye_by when it exits.
- Note that atexit only removes the first occurence of a function from the list, so if a function was placed in the list multiple times with atexit, it must also be removed from the list multiple times.
Приложения с графическим интерфейсом
Кнопка, элемент управления, флажок
# создаем фигуру и панно на нейж = фигура;# создаем кнопку (стиль по умолчанию)b1 = uicontrol (ж, "строка", "Кнопка", "должность",);# создать элемент редактированияe1 = uicontrol (ж, "стиль", "редактировать", "строка", "редактируемый текст", "должность",);# создать флажокc1 = uicontrol (ж, "стиль", "флажок", "строка", "флажок", "должность",);
Текстовое окно
незамедлительный = {"Ширина", "Рост", «Глубина»};значения по умолчанию = {"1.10", "2.20", "3.30"};ряды = 1,10; 2,20; 3,30];тускнеет = inputdlg (незамедлительный, «Введите размеры коробки», ряды, значения по умолчанию);
Список с окнами сообщений.
my_options = {"Пункт", "еще один", "еще один"};сел, ОК = listdlg ("ListString", my_options, "SelectionMode", "Множественный");если (ОК == 1) msgbox ("Вы выбрали:"); для я = 1число (сел) msgbox (спринт (" t% s", my_options{сел(я)})); конецеще msgbox ("Вы отменили".);endif
Радио-кнопки
# создаем фигуру и панно на нейж = фигура;# создаем группу кнопокGP = uibuttongroup (ж, "Должность", 0.5 1 1])# создаем кнопки в группеb1 = uicontrol (GP, "стиль", "переключатель", "строка", «Выбор 1», "Должность", 10 150 100 50 ]);Би 2 = uicontrol (GP, "стиль", "переключатель", "строка", «Выбор 2», "Должность", 10 50 100 30 ]);# создаем кнопку не в группеb3 = uicontrol (ж, "стиль", "переключатель","строка", «Не в группе»,"Должность", 10 50 100 50 ]);
[править] Переменные
Синтаксис:
Поскольку GNU Octave считается языком высокого уровня, к определению переменных выставляются определенные требования:
- название переменной может содержать буквы, цифры и символы подчеркивания «_», но не должно начинаться с цифры;
- язык GNU Octave чувствителен к регистру, т.е. А и а — это разные переменные;
- создавать переменные можно в любом месте программы (они не описываются и не объявляются);
- переменные не имеют «постоянства» типа данных, т.е., сначала можно присвоить а=10, а потом а=»Hello!»;
Как и в обычных языках программирования, переменные Octave подразделяются на глобальные (определенные в файлах-сценариях) и локальные (определенные в файлах-функциях). Рассмотрим следующий пример. Пусть результаты расчетов (в данном случае, присваивание значений переменным а и b) «главной» программы Script1 передаются в подпрограмму Script2, а та, в свою очередь, выполняет над ними какие-то действия и вызывает функцю function MyFunction().
Пример 1.
В результате вызова трех m-файлов, значения переменных останутся а=2 и b=2. Дело в том, что переменные объявленные в функции считаются локальными, т.е. они создаются при обращении к MyFunction и удаляются из памяти при выходе из нее
Переменные же созданные в скриптах «живут» до тех пор, пока не будет выполнен весь набор команд (неважно, размещены ли эти команды в одном или разных файлах). И более того, значения глобальных переменных сохраняются на протяжении всего сеанса работы с Octave, т.е
они доступны даже в абсолютно разных программах, запускаемых последовательно не выходя из системы. Таким образом, в приведенном выше примере по сути созданы две разных пары переменных с одинаковыми именами — одна пара а и b существует вне определения функций, вторая ее копия — сугубо в пределах function .. endfunction.
Global декларация переменных
Как было указано выше, пространства переменных скриптов и функций не пересекаются между собой. Однако существует возможность из функции обратиться к глобальной переменной для использования ее значения (как чтения, так и изменения). Реализуется такая возможность посредством ключевого слова global.
Пример 2.
Entering commands[edit | edit source]
The last line above is known as the Octave prompt and, much like the prompt in Linux, this is where you type Octave commands. To do simple arithmetic, use (addition), (subtraction),
(multiplication), (division), and (exponentiation).
Many mathematical functions are available and have obvious names (with many of those similar to other programming languages). For example, we have:
- trigonometric functions: , ,
- inverse trigonometric functions: , ,
- natural and base 10 logarithms: ,
- exponentiation:
- absolute value:
Various constants are also pre-defined: , (Euler’s number), and (the imaginary number sqrt(-1)), (Infinity), (Not a Number — resulting from undefined operations, such as .)
Here are some examples showing the input typed at the prompt and the output returned by Octave.
| 2+3{\displaystyle 2+3} | log10100log1010{\displaystyle {\frac {\log _{10}100}{\log _{10}10}}} | ⌊1+tan1.21.2⌋{\displaystyle \left\lfloor {\frac {1+\tan 1.2}{1.2}}\right\rfloor } | 32+42{\displaystyle {\sqrt {3^{2}+4^{2}}}} |
octave:1> 2 + 3 ans = 5 |
octave:2> log10(100)/log10(10) ans = 2 |
octave:3> floor((1+tan(1.2)) / 1.2) ans = 2 |
octave:4> sqrt(3^2 + 4^2) ans = 5 |
| ei⋅π{\displaystyle e^{i\cdot \pi }} |
octave:5> e^(i*pi) ans = -1.0000e+00 + 1.2246e-16i octave:6> # Comment: From Euler's famous formula octave:6> # extremely close to the correct value of -1 |
Some things to note:
- Octave requires parentheses around the input of a function (so, is fine, but () is not).
- Any spacing before and after arithmetic operators is optional, but allowed.
- Not all Octave functions have obvious names (e.g. above). Don’t panic for now. You will get to know them as we go along.
How do I install or load all Octave Forge packages?[edit]
Do not do it! Really, there is no reason to do this. Octave has many packages for different needs and is unlikely that you need all of them. You either have a small set of required packages, in which case
you know them by name; or you want them all «just because», in which case you don’t really need them.
The common misconception is that the more packages one has installed and loaded, the more complete and powerful its Octave installation will be. However, in the same way one would never install all perl modules, ruby gems, python packages, and C++ libraries (because it simply makes no sense), one should not install all Octave packages.
Packages should be installed and loaded selectively. Note that some packages are meant to shadow core functions changing the way Octave works, and that different packages can have different functions with the same name leading to unpredictable results.
If you really really really want to do load all packages, you can with the following:
## WARNING: loading all packages is probably not the solution you are looking for.
cellfun (@(x) pkg ("load", x.name), pkg ("list"));
Простые примеры
Рассмотрим несколько простых примеров, чтобы максимально быстро войти в курс дела и понять как все тут работает. Взято с документации.
Элементарные вычисления
Octave поддерживает следующие арифметические операции + - * , возведение в степень ^, натуральные логарифмы/показатели (log, exp), тригонометрические функции (sin, cos, …). Кроме этого, Octave может работать как с вещественными числами, так и с комплексными (i, j). Также предопределены некоторые математические константы, например, число pi и основание натурального логарифма e.
Попробуем для начала проверить тождество Эйлера.
Вводим в командное окно следующее выражение:
>> exp(i*pi)
Ответ должен быть равен -1, я у себя получил следующее:
ans = -1.0000e+00 + 1.2246e-16i
Создание матриц
Векторы и матрицы базовые строительные блоки числового анализа. Для создания матрицы и сохранения ее в переменную для последующего использования нужно ввести следующую команду:
>> A =
И получим ответ:
A =
1 1 2
3 5 8
13 21 34
Если ввести команду, поставив в конце точку с запятой, то Octave не будет выводить матрицу на экран, например, создадим матрицу на 3 строки и 2 столбца со случайными числами:
>> B = rand (3, 2);
Теперь для того, чтобы получить вывод данной матрицы на экран, достаточно ввести в командное окно имя переменной, в которой она сохранена:
>> B
Арифметика матриц
Умножение матрицы на скаляр:
>> 2 * A
Перемножение двух матриц:
>> A * B
Умножение транспонированной матрицы на саму себя:
>> A' * A
Решение систем линейных уравнений
Разберем на примере следующего уравнения
Распишем матрицы коэффициентов и свободных членов для этой системы уравнений
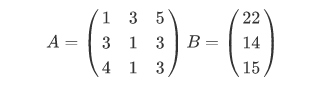
Теперь набираем обе получившиеся матрицы в Octave и решаем систему методом наименьших квадратов с помощью, так называемого оператора левого деления \
>> A = ; >> B = ; >> A\B ans = 1.0000 2.0000 3.0000
Решение нелинейных дифференциальных уравнений
Octave может проинтегрировать уравнения следующего вида
Пробуем ввести функцию в Octave, сделать это несложно, гораздо сложнее понять, что ты только что сделал) Я уже давно забыл всю теорию вышмата, так что просто повторил пример и это работает, позже уже буду разбираться как.
>> function xdot = f (x, t)
r = 0.25;
k = 1.4;
a = 1.5;
b = 0.16;
c = 0.9;
d = 0.8;
xdot(1) = r*x(1)*(1 - x(1)/k) - a*x(1)*x(2)/(1 + b*x(1));
xdot(2) = c*a*x(1)*x(2)/(1 + b*x(1)) - d*x(2);
endfunction
>> x0 = ;
>> t = linspace (0, 50, 200)';
>> x = lsode ("f", x0, t);
Последняя команда производит интегрирование и если ее выполнить без ; в конце, то можно будет увидеть много цифр рассчитанной функциональной зависимости.

Графический вывод
Чтобы получить график, полученного в прошлом примере решения достаточно ввести команду:
>> plot (t, x)
Octave тут же создаст новое окно с вот таким вот красивым графиком, который к тому же можно сохранить скажем в pdf формат командой:
>> print -dpdf ~/foo.pdf
Пока на этом все, буду стараться использовать Octave в разработке и если у меня будет получаться, то я непременно напишу об этом в блоге. А пока подписывайтесь куда-нибудь (ВК, Твиттер), что-нибудь жмите, что-нибудь пишите (Телеграм). Всем пока!
использованная литература
Источники
- Аллен, Дэвид. 1967. «Октавная различимость музыкальных и немузыкальных предметов». Психономическая наука 7: 421–22.
- Блэквелл, HR, и Х. Шлосберг. 1943. «Обобщение октав, различение высоты тона и пороги громкости у белой крысы». Журнал экспериментальной психологии 33: 407–419.
- Cynx, Джеффри. 1996. «Нейроэтологические исследования того, как птицы различают песни». В нейроэтологии когнитивных и перцептивных процессов , под редакцией К. Ф. Мосса и С. Дж. Шаттлворта, 63. Боулдер: Westview Press.
- Демани, Лоран и Франсуаза Арман. 1984. «Реальность восприятия цветности тона в раннем младенчестве». Журнал Акустического общества Америки 76: 57–66.
- Сержант, Десмонд. 1983. «Октава: восприятие или концепция?» Психология музыки 11, вып. 1: 3–18.
How do I change color/line definition in gnuplot postscript?[edit]
Here is a awk script to get a rainbow color map
#!/bin/awk -f
BEGIN {
split("0 4 6 7 5 3 1 2 8", rainbow, " ");
split("7 3 1 0 2 4 6 5 8", invraim, " ");
}
$1 ~ /\/LT/ {
n = substr($1, 4, 1);
if (n == 0)
lt = "{ PL [] 0.9 0.1 0.1 DL } def";
else if (n == 1)
lt = "{ PL 0.1 .75 0.1 DL } def";
else if (n == 2)
lt = "{ PL 0.1 0.1 0.9 DL } def";
else if (n == 3)
lt = "{ PL 0.9 0 0.8 DL } def";
else if (n == 4)
lt = "{ PL 0.1 0.8 0.8 DL } def";
else if (n == 5)
lt = "{ PL 0.9 0.8 0.2 DL } def";
else if (n == 6)
lt = "{ PL 0.5 0.3 0.1 DL } def";
else if (n == 7)
lt = "{ PL 1 0.4 0 DL } def";
else if (n == 8)
lt = "{ PL 0.5 0.5 0.5 DL } def";
$0 = sprintf("/LT%d %s", rainbow, lt);
##$0 = sprintf("/LT%x %s", invraim, lt);
##$0 = sprintf("/LT%x %s", n, lt);
}
{ print; }
Что-же дальше?
Может возникнуть вопрос: а зачем вообще нужны открытые математические пакеты? Офисные приложения нужны всем, но ведь далеко не каждому необходимо сидя дома решать уравнения Пуассона, с помощью преобразования Лапласа. Для ВУЗ-ов стоит значительно дешевле, нежели для физических лиц и коммерческих организаций. Коммерческие организации, если будет нужно, найдут денежные средства, а обычные люди пусть занимаются математикой в университетах или считают столбиком.
Конечно же, это ошибочное мнение. Научные расчеты, выполненные с использованием открытого ПО имеют дополнительный «уровень защиты», ведь при желании любой может повторить прогнать те же самые расчеты и проверить валидность результатов. Те же самые вычисления, выполненные на дорогущем ПО, частично отсекают возможность проверки результатов. Проблема на самом деле гораздо шире (английский текст) и дело не только в открытых или проприетарных математических программах. Не секрет, что научные журналы как правило не требуют от авторов предоставить данные и методику, достаточные для гарантированного повтора результатов эксперимента, проверки модели. Особенно часто этим грешат экономисты и финансисты, попросту засекречивая свои данные. Проверка расчетов и выводов среди выборки из массива статей с «засекреченными» данными дала неожиданные результаты (английский текст). Наука, как и софт, должна быть открытой, вот почему открытые математические пакеты имеют ценность для всего общества.
Рекомендуется к прочтению
Кроме последней книги, остальные материалы, использованные в статье, можно без труда найти в интернете. Половина из приведенных выше ссылок ведут на английские страницы. Буду рад вкратце сообщить о чем идет там речь или помочь с переводом.
High-Level Overview
There are three separate components of Octave Online Server:
- Client: Code that runs in the browser.
- Front Server: Authentication, client session handling.
- Back Server: File I/O, Octave process handling.
Scaling: Front Servers and Back Servers can be scaled independently (in general, you need more Back Servers than Front Servers). It is also possible to run both the Front Server and the Back Server on the same computer.
Languages: All code is written with JavaScript technologies, although for historical reasons, the three components use different flavors of JavaScript. The Client uses ES5; the Front Server uses TypeScript; and the Back Server uses ES6.
Создание матрицы[править]
Чтобы создать новую матрицу и сохранит её в переменной, введите команду:
octave1>A=1,1,2;3,5,8;13,21,34
Octave выведет на экран матрицу с аккуратно выровненными колонками. Если команду закончить «;», то Octave не будет выводить результат команды. Например, команда:
octave2>B=rand(3,2);
создаст матрицу с 3 строками и 2 столбцами, элементы которой примут случайные значения в промежутке между нулём и единицей.
Чтобы отобразить значение любой переменной, просто напишите имя переменной. Например, чтобы отобразить значения, хранящиеся в матрице B, наберите команду:
octave3>B
Why is Octave’s floating-point computation wrong?[edit]
Floating-point arithmetic is an approximation in binary to arithmetic on real or complex numbers. Just like you cannot represent 1/3 exactly in decimal arithmetic (0.333333… is only a rough approximation to 1/3 for any finite number of 3s), you cannot represent some fractions like 110{\displaystyle 1/10} exactly in base 2. In binary, the representation to one tenth is 0.00011¯b{\displaystyle 0.0{\overline {0011}}_{b}} where the bar indicates that it repeats infinitely (like how 16=0.16¯d{\displaystyle 1/6=0.1{\overline {6}}_{d}} in decimal). Because this infinite repetition cannot be represented exactly with a finite number of digits, rounding errors occur for values that appear to be exact in decimal but are in fact approximations in binary, such as for example how 0.3 — 0.2 — 0.1 is not equal to zero.
Another approach to deal with rounding errors is interval arithmetic with the Interval package or symbolic computations with the Symbolic package. These approaches are likely to be slower, since not all operations can be performed on Hardware like pure floating-point arithmetic.
Пример[править]
Сейчас мы построим графики, изображенные на рисунках 3 и 4.
На рисунке 3 изображены три тригонометрические функции
- cos2x{\displaystyle \cos 2x},
- sin4x{\displaystyle \sin 4x}, and
- 2sinx{\displaystyle 2\sin x}
на одном множестве осей. На рисунке 4 показан график суммы этих функций.
Первым делом, используем функцию , чтобы создать вектор X-значений
octave:1> x = linspace(0, 2*pi);
Затем посчитаем Y-значения для всех трёх функций
octave:2> a = cos(2*x); octave:3> b = sin(4*x); octave:4> c = 2*sin(x);
Следующие команды построят график всех трёх функций
octave:5> figure; octave:6> plot(x, a); octave:7> hold on; octave:8> plot(x, b); octave:9> plot(x, c);
На строке 5 () мы сообщаем Octave, что хотим построить новый график в новом окне. Считается хорошей практикой вызывать перед построением нового графика
Такой подход помогает избежать случайно замены предыдущего важного графика.
Обратите внимание, что на строке 7, используется команда , чтобы сообщить Octave, что мы не хотим замещать предыдущий график (со строки 6) последующими. Octave, после использования , будет строить все последующие графики на той же плоскости, пока не будет вызвана команда .. Форма, которую вы видите, отображает все три построенные функции одинаковым цветом
Чтобы заставить Octave задать различные цвета автоматически, постройте все функции за один шаг:
Форма, которую вы видите, отображает все три построенные функции одинаковым цветом. Чтобы заставить Octave задать различные цвета автоматически, постройте все функции за один шаг:
octave:10> plot(x, a, x, b, x, c);
Ну, и наконец-то, построим второй график (рисунок 4):
octave:11> figure; octave:12> hold off; octave:13> plot(x, a+b+c);
Строка 11 создает новое окно, а строка 12 сообщает Octave, что все последующие построения графиков будут просто замещать предыдущие. На строке 13 мы строим график суммы всех функций.
Октава, язык
Программы Octave состоят из списка вызовов функций или сценария . Синтаксис основан на матрице и предоставляет различные функции для матричных операций. Он поддерживает различные структуры данных и позволяет объектно-ориентированное программирование .
Его синтаксис очень похож на MATLAB, и тщательное программирование скрипта позволит ему работать как в Octave, так и в MATLAB.
Поскольку Octave предоставляется под Стандартной общественной лицензией GNU , ее можно свободно изменять, копировать и использовать. Программа работает в Microsoft Windows и большинстве Unix и Unix-подобных операционных систем , включая Linux , Android и macOS .
Совместимость с MATLAB
Octave был построен с учетом совместимости с MATLAB и имеет много общих функций с MATLAB:
- Матрицы как фундаментальный тип данных.
- Встроенная поддержка комплексных чисел.
- Мощные встроенные математические функции и обширные библиотеки функций.
- Расширяемость в виде пользовательских функций.
Octave рассматривает несовместимость с MATLAB как ошибка; следовательно, это можно было бы считать клон программного обеспечения, что не нарушает авторское право на программное обеспечение согласно Лотус против Borland судебное дело.
Скрипты MATLAB из MathWorksРепозиторий FileExchange в принципе совместим с Octave. Однако, хотя они часто предоставляются и загружаются пользователями под Octave совместимый и собственно Открытый исходный код Лицензия BSD, файловый обмен Условия эксплуатации запретить любое использование кроме MathWorks ‘ проприетарный MATLAB.
Совместимость синтаксиса
- Комментарий строки могут начинаться с символа #, а также символа%;
- Различный На основе C операторы ++, —, +=, * =, / = поддерживаются;
- На элементы можно ссылаться без создания новой переменной путем каскадного индексирования, например (3);
- Струны может быть определен как символ двойной кавычки, так и символ одиночной кавычки;
- Когда тип переменной не замужем (число с плавающей запятой одинарной точности) Octave вычисляет «значить»в однодоменном (MATLAB в двойной домен) что быстрее, но дает менее точные результаты;
- Блоки также могут быть завершены более конкретными Структура управления ключевые слова, то есть endif, endfor, end while и т. д .;
- Функции могут быть определены в сценариях и в приглашении Octave;
- Наличие цикла do-until (аналогично делать пока в C).
Совместимость функций
Когда вызывается нереализованная функция, отображается следующее сообщение об ошибке:
октава1> руководство предупреждение то 'руководство' функция является не еще реализовано в Октава Пожалуйста читать <http//www.октава.orgотсутствует.html> к учить Как ты мочь делать вклад отсутствует функциональность. ошибка 'руководство' неопределенный около линия 1 столбец 1
[править] Служебные символы
| # | — комментарий в программе |
| . | — разделитель целой и дробной части числа; разделитель различных выражений (например, см. структуры данных) |
| , | — в скриптах — разделитель нескольких операторов в строке; в описании функции — разделитель переменных; в массивах — разделитель строк |
| ; | — в скриптах — блокирование вывода на экран результата; в массивах — разделитель столбцов |
| … | — неразрывный перенос строки — при вводе элементов массивов, если недостаточно места в текущей |
| GNU Octave
Инсталляция | |
|---|
Troubleshooting
Kernel Times Out While Starting
If the kernel does not start, run the following command from a terminal:
python -m octave_kernel.check
This can help diagnose problems with setting up integration with Octave. If in doubt,
create an issue with the output of that command.
Kernel is Not Listed
If the kernel is not listed as an available kernel, first try the following command:
python -m octave_kernel install --user
If the kernel is still not listed, verify that the following point to the same
version of python:
which python # use "where" if using cmd.exe which jupyter
Octave-Snap (Linux)
You can check if you are using a snap version on Linux by checking the path to your Octave
installation.
which octave
If the returned path has in it, then Octave is running in a container and you will need to configure the kernel appropriately.
- Set the environment variable
echo export OCTAVE_EXECUTABLE=\"octave\" >> ~/.bashrc
- Make a directory for the temporary plot directories that the kernel uses. This cannot be a hidden directory.
mkdir ~/octavePlots
- Set to point to your plot directory in .
c.OctaveKernel.plot_settings = dict(plot_dir='<home>/octavePlots')
where is the absolute path to your home directory. Do not use as this resolves to a different location for Octave-Snap.
Blank Plot
Specify a different format using the magic or using a configuration setting.
On some systems, the default produces a black plot. On other systems produces a
black plot.