Начертательная геометрия

Задачи и решения

Задача 1. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетов равна 26.4см. Найдите гипотенузу треугольника.

Решение. Обозначим через b− меньший катет, а через c− гипотенузу. Из условия задачи имеем: c+b=26.4см.

Так как один из острых углов прямоугольного треугольника равен 60°, то другой острый угол равен 90°−60°=30°. Как известно, против угла 60° лежит большая сторона (катет), а против угла 30° − меньшая. Из свойства 2 следует, что меньшая сторона равна половине гипотенузы : . Тогда имеем: или . Следовательно c=17.6 см.

Ответ: 17.6 см.

Задача 2. В треугольниках ABC и A₁B₁C₁, углы A и A₁ прямые, BD и B₁D₁ −биссектрисы. Докажите, что , если и BD=B₁D₁.

Доказательство. Так как BD и B₁D₁ −биссектрисы и , то (Рис.8). Из и следует, что (Теорема 1).

Тогда и, следовательно, . Отсюда получим, что треугольники BDC и B₁D₁C₁ равны (второй признак равенства треугольников:, , ). Следовательно (так как , ).

Znanija — приложение, которое поможет решить уравнение по геометрии

На сайте znanija.com пользователи могут выкладывать фотографии с геометрическими задачками. Это русскоязычный сегмент проекта brainly.com. Он позволяет ученикам обращаться за квалифицированной помощью специалистов со всего мира.

Вы можете найти приложение «Знания» по запросу «Brainly» на платформе App Store или Google Play. Скачайте эту программу на свой телефон, чтобы пообщаться с экспертами и отличниками.

Основные достоинства приложения для решения сложных задач по геометрии:

Преимущества приложения:	Пояснения:
Здесь разбирающиеся в предмете люди могут оказать посильную помощь тем, кто в этом нуждается.	Набирайте за это баллы и получайте увеличение статуса. Чтобы увидеть размер вознаграждения, посмотрите на иконку в правом верхнем углу от вопроса. Наведите на нее курсор, и вы сможете узнать больше о системе баллов.
Если не хотите ожидать ответа, воспользуйтесь поиском по архиву.	В библиотеке «Знания» накопилось уже немало готовых решений задач. Наверняка там найдется и нужная вам информация.
В приложении есть встроенные покупки.	Однако цена годовой подписки на App Store сравнительно невелика.
Сообщество работает круглосуточно.	Пользователи проживают в разных часовых поясах, поэтому могут отвечать на вопросы в любое время.

Для записи геометрических функций и математических знаков работает клавиатура LaTeX.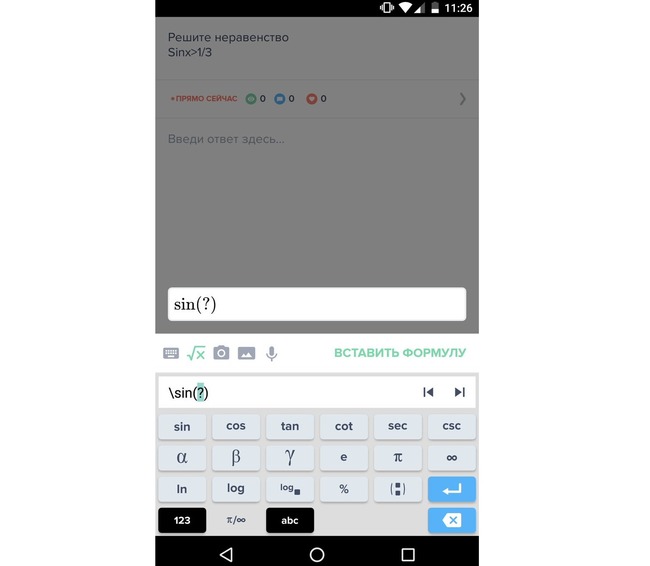

В приложении можно получить помощь по всем базовым предметам, включая геометрию. Доступны такие языки как украинский, казахский, белорусский.

Чтобы вас не ввели в заблуждение, эксперты сообщества просматривают ответы к задачам и оставляют пометку «Проверенный». Если вы ее увидите, то можете полагаться на такой комментарий.

Ответы находятся очень быстро. Решение большинства задач по геометрии находится в течение первых 10 минут с момента загрузки фото в приложение. Однако на всякий случай постарайтесь скидывать снимки заранее. Даже если вы получите ответ сразу, у вас останется больше времени на то, чтобы понять объяснение и подготовиться к уроку.

Построение параллельных (непересекающихся) прямых

Имеется прямая и т. А, не лежащая на этой прямой.

Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.

Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.

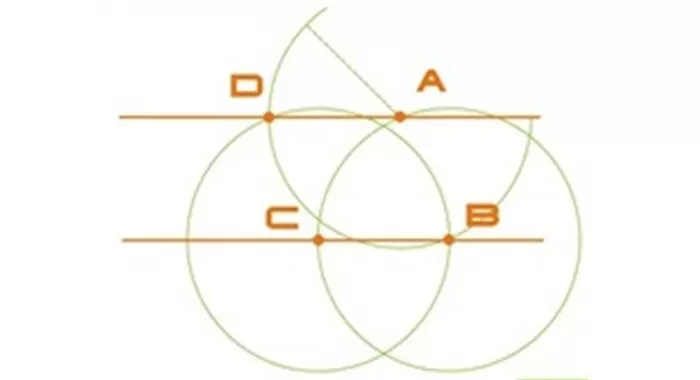
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.

C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.

Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.

Задача решена.

Свойства треугольников

Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.

Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника. Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет

Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок

Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.

Неравенство треугольника Сумма любых двух сторон треугольника больше его третьей стороны.

Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.

Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.

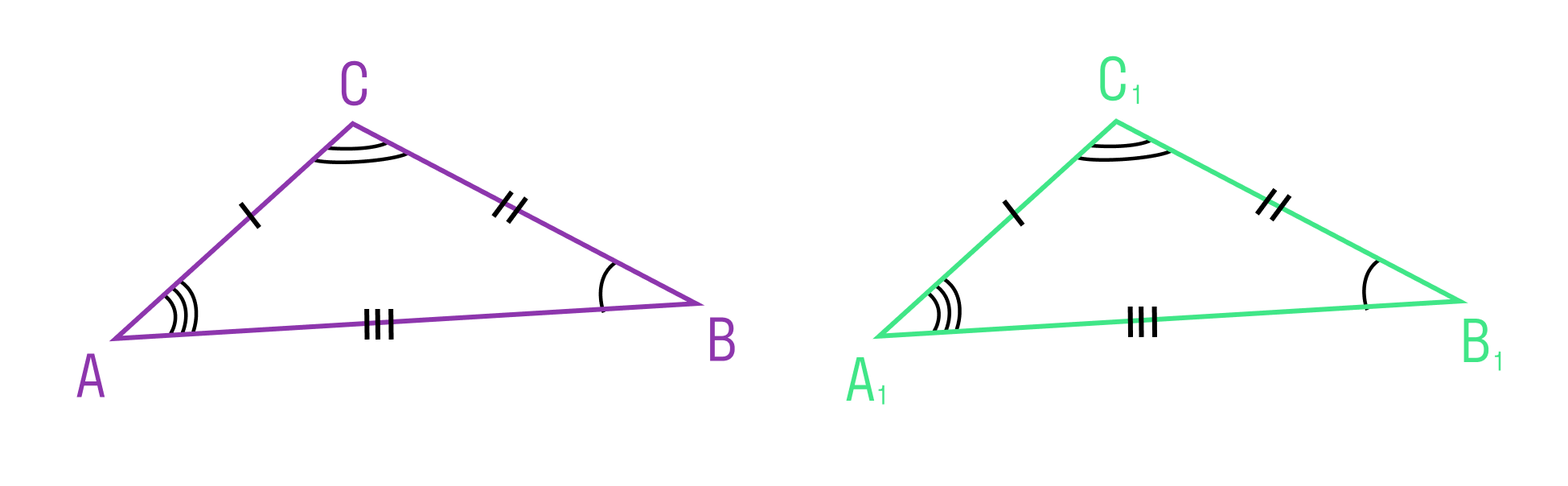
Равенство треугольников ABC и A₁B₁C₁ обозначается так: ΔABC = ΔA₁B₁C₁.

Есть даже специальные теоремы про равенство треугольников.

Первый признак равенства треугольников звучит так:

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны

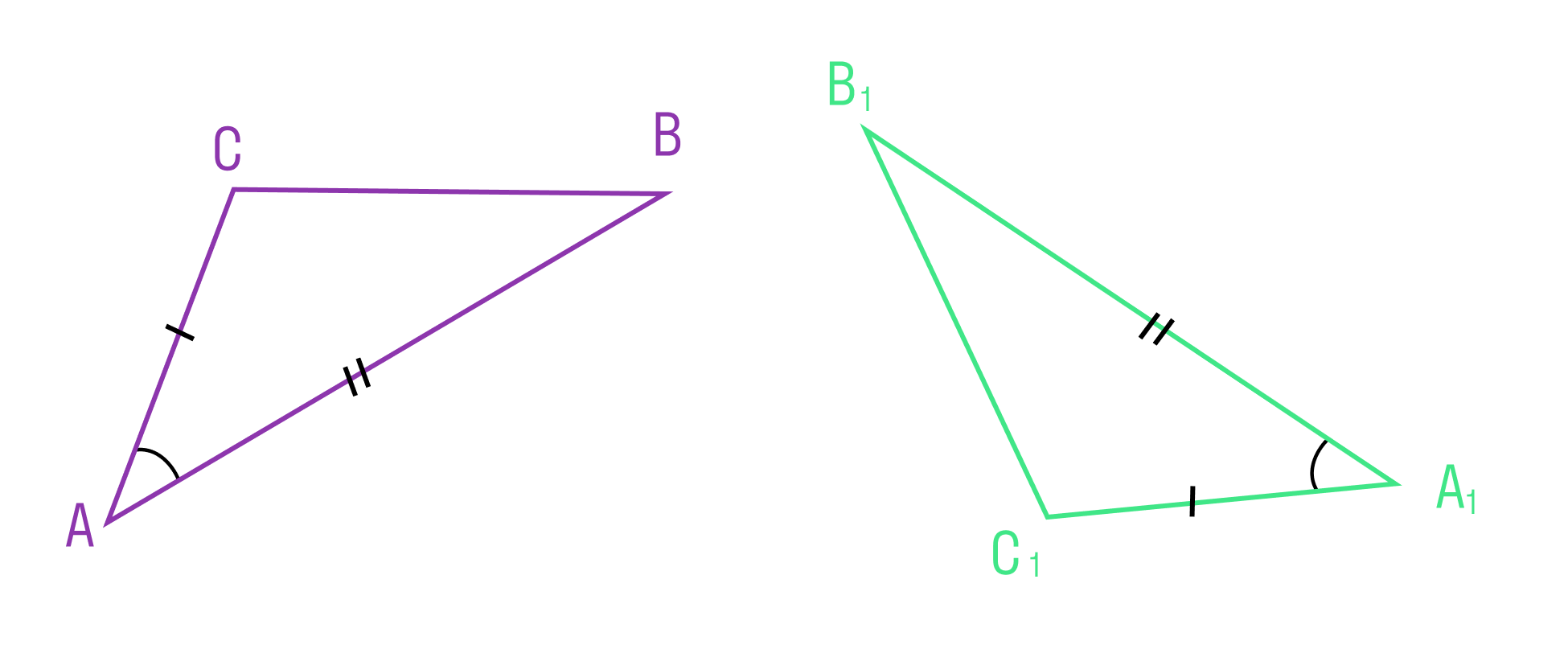
ΔABC = ΔA₁B₁C₁, так как AC = A₁C₁, AB = A₁B₁ и ∠A = ∠A₁ (∠A лежит между сторонами AC и AB, а ∠A₁ между A₁C₁ и A₁B₁).

Второй признак равенства треугольников

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

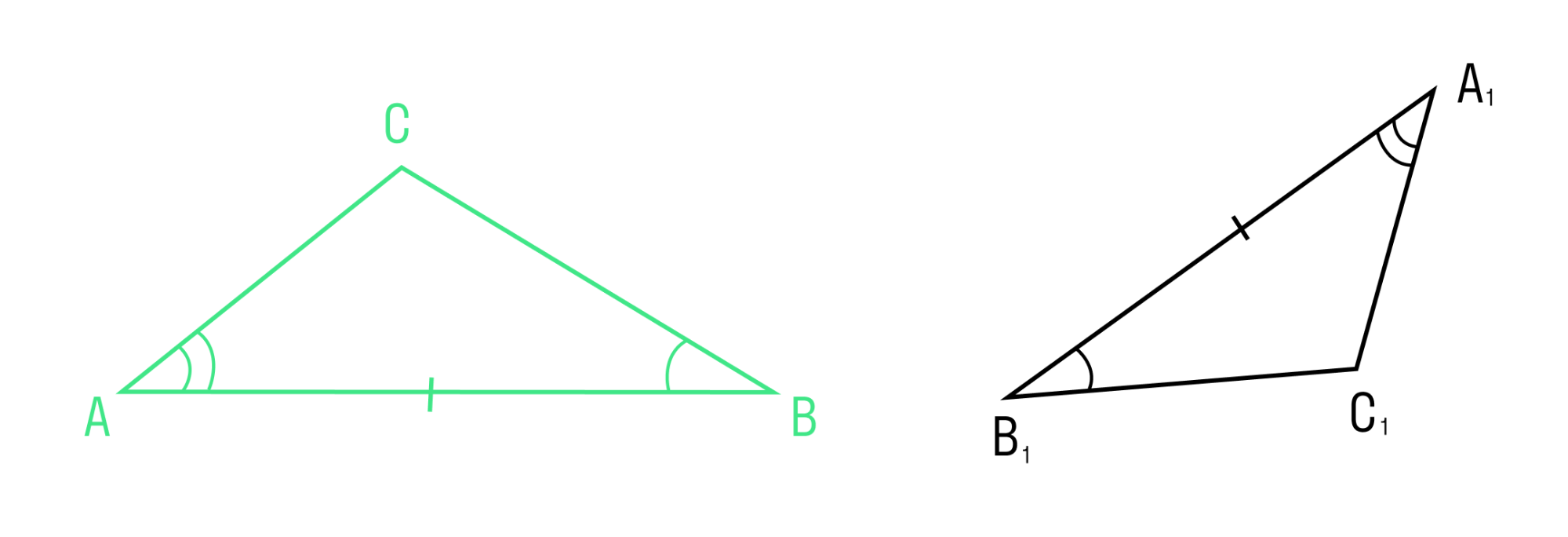
ΔABC = ΔA₁B₁C₁, так как AB = A₁B₁,  ∠A = ∠A₁, ∠B = ∠B₁.

Третий признак равенства треугольников

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

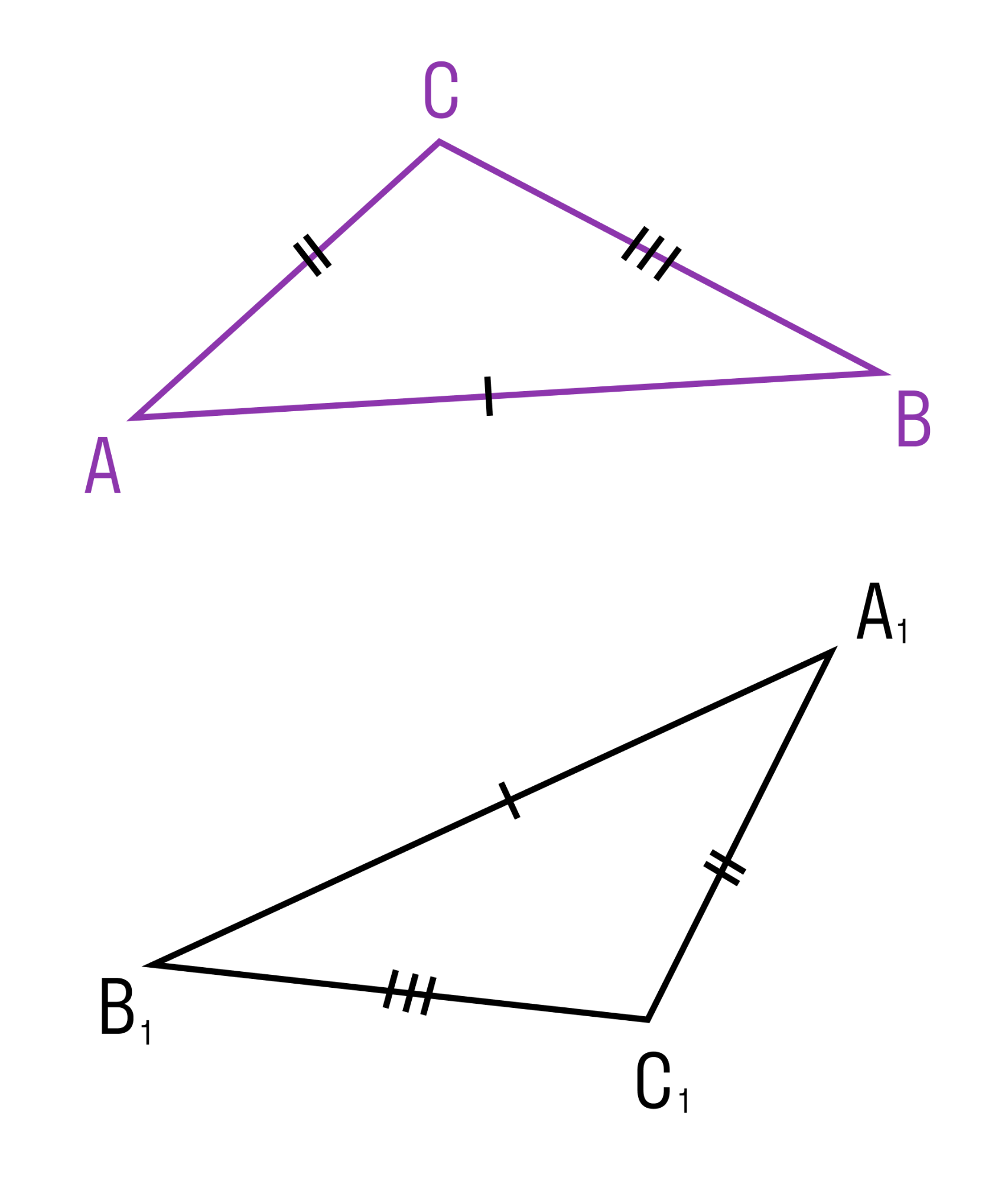
ΔABC = ΔA₁B₁C₁, так как AC = A₁C₁, AB = A₁B₁ и BC = B₁C₁.

Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.

Классификация треугольников по их сторонам

Для классификации треугольников можно использовать их типологию.

Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.

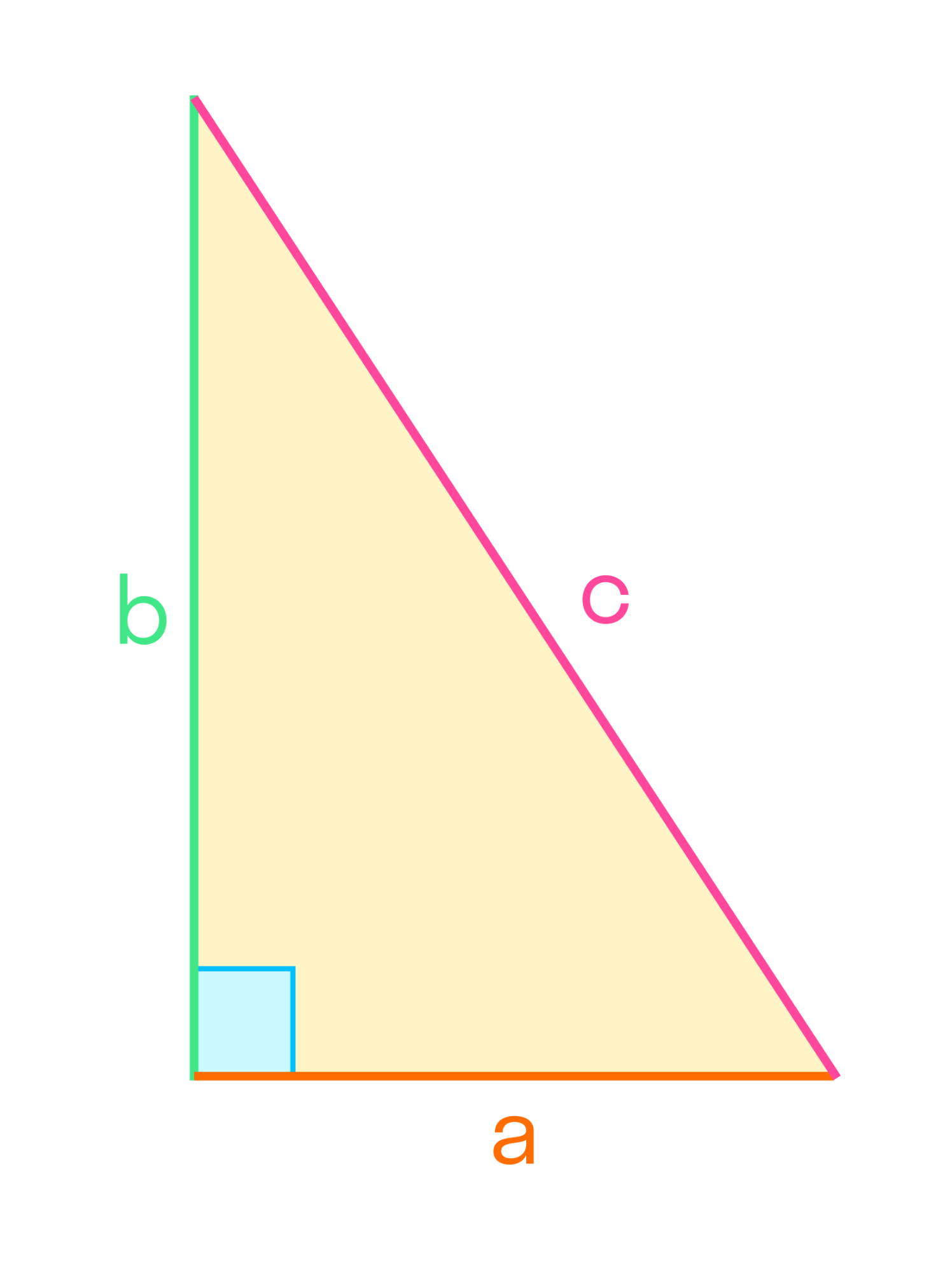
Свойства прямоугольного треугольника

1. Теорема Пифагора сумма длин квадратов катетов равна квадрату гипотенузы
2. Свойство медианы: медиана, проведенная из вершины с прямым углом, равняется половине гипотенузы.

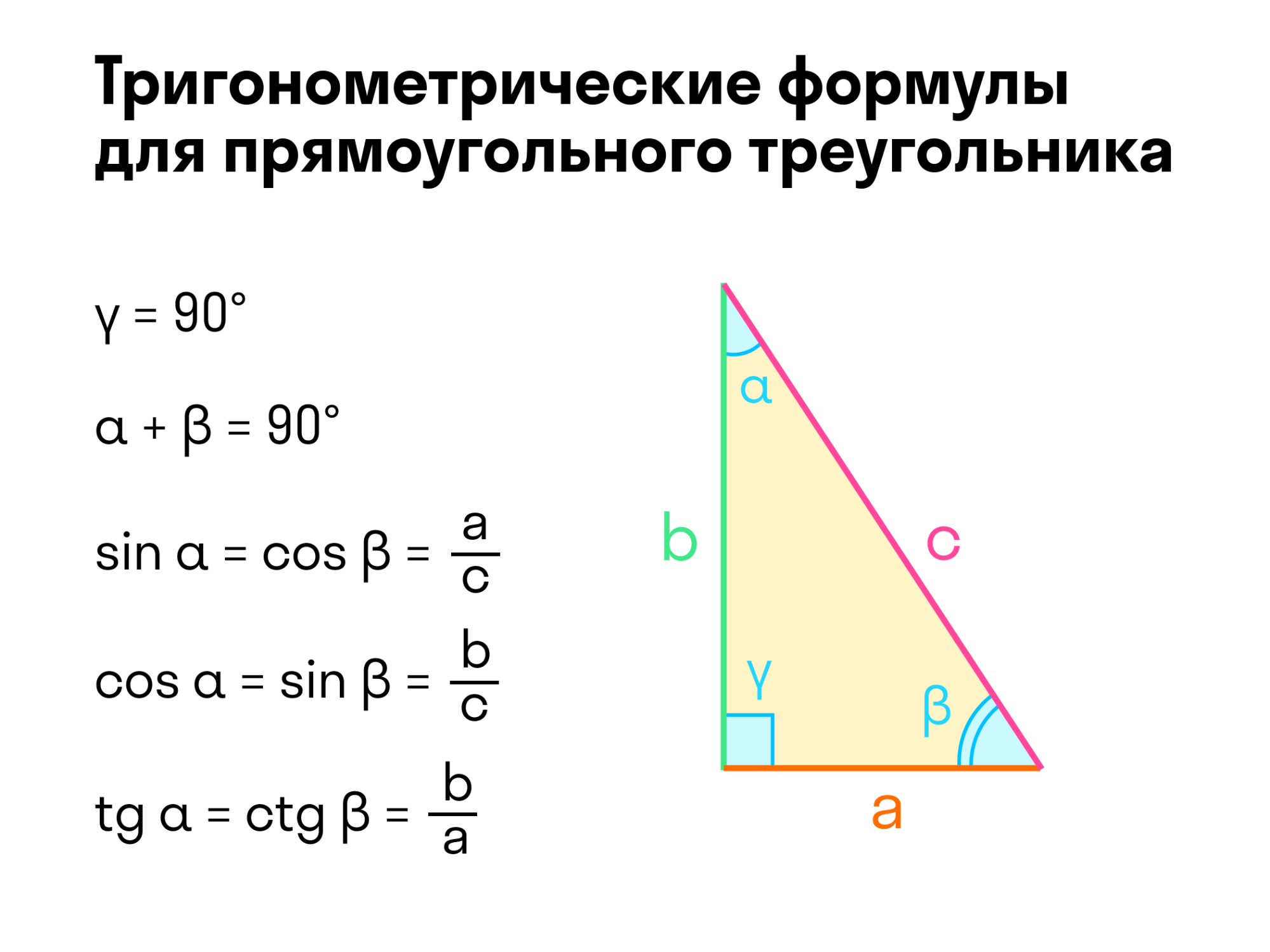
С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.

Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.

Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.

Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.

От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов

Расширение GeoGebra

Создано расширение GeoGebra для браузера Google Chrome

Обратите внимание на количество пользователей расширения: более 2.6 миллиона человек. Немногие расширения из магазина Chrome могут сравниться с такими цифрами

Это свидетельствует о том, что приложение GeoGebra широко используется в мире для образовательных целей.

Для входа в расширение кликните по кнопке «Сервисы» на панели закладок в браузере Google Chrome. После этого будет открыто окно расширения GeoGebra в вашем браузере. На начальном экране вы можете выбрать раздел математики, с которым далее вы будете работать в приложении.

Дополнительные материалы по работе в программе, вы можете найти на сайте производителя приложения, и в интернете.

Программы для черчения

Также при описании онлайн сервисов для создания эскиза проекта, нельзя обойти стороной и ряд популярных программ, созданных специально для таких целей. При этом большинство из них обладает платным характером, так как для решения профессиональных задач функционала бесплатных программ может быть недостаточно.

• «Autodesk AutoCAD» — одна из наиболее известных систем автоматизированного проектирования (САПР), предназначенных для создания различных видов чертежей, схем, графиков. Позволяет создавать 2Д и 3Д чертежи на высокопрофессиональном уровне, обладает богатым функционалом, отлично справляется с рендерингом 3Д-объектов, умеет работать с 3Д-принтером. Поддерживается работа с чертежами в формате DVG, DWF, DXF;
• «Аскон Компас» — это целый комплекс программных решений для осуществления черчения и диаграмм, довольно популярных на территории РФ. Данные решения поддерживают множество форматов электронных чертежей, обладают большой базой присоединяемых библиотек, при этом довольно просты и удобны в работе;
• «nanoCAD» — бесплатная программа для начинающих, включающая необходимый набор базовых инструментов для осуществления проектирования и создания чертежей. Программа направления на создание преимущественно 2Д-чертежей, поддерживает работу с DWG и DXF чертежами, достоинством программы является быстрый вывод объектов, работы с DirectX и так далее.

Ввод данных и функционал

• В качестве элементов используются обыкновенные правильные дроби (, , ), десятичные дроби (, , ), а также числа в экспоненциальной форме (, ).
• Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
• Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
• Вставляйте результат в A или B с помощью кнопок «Вставить в A» и «Вставить в B».
• Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
• Используйте стрелки (, , , ) для перемещения по элементам

Практическая сторона геометрии

Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.

Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.

А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.

Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.

Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.

Почему изучать геометрию сложно: некоторые правила придется учить наизусть.

Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество

Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней

Базовые геометрические объекты

Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.

Точка — это идеальный математический объект, у которого нет длины и ширины.

Отрезок — это часть прямой, у которого есть начало и конец.

Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.

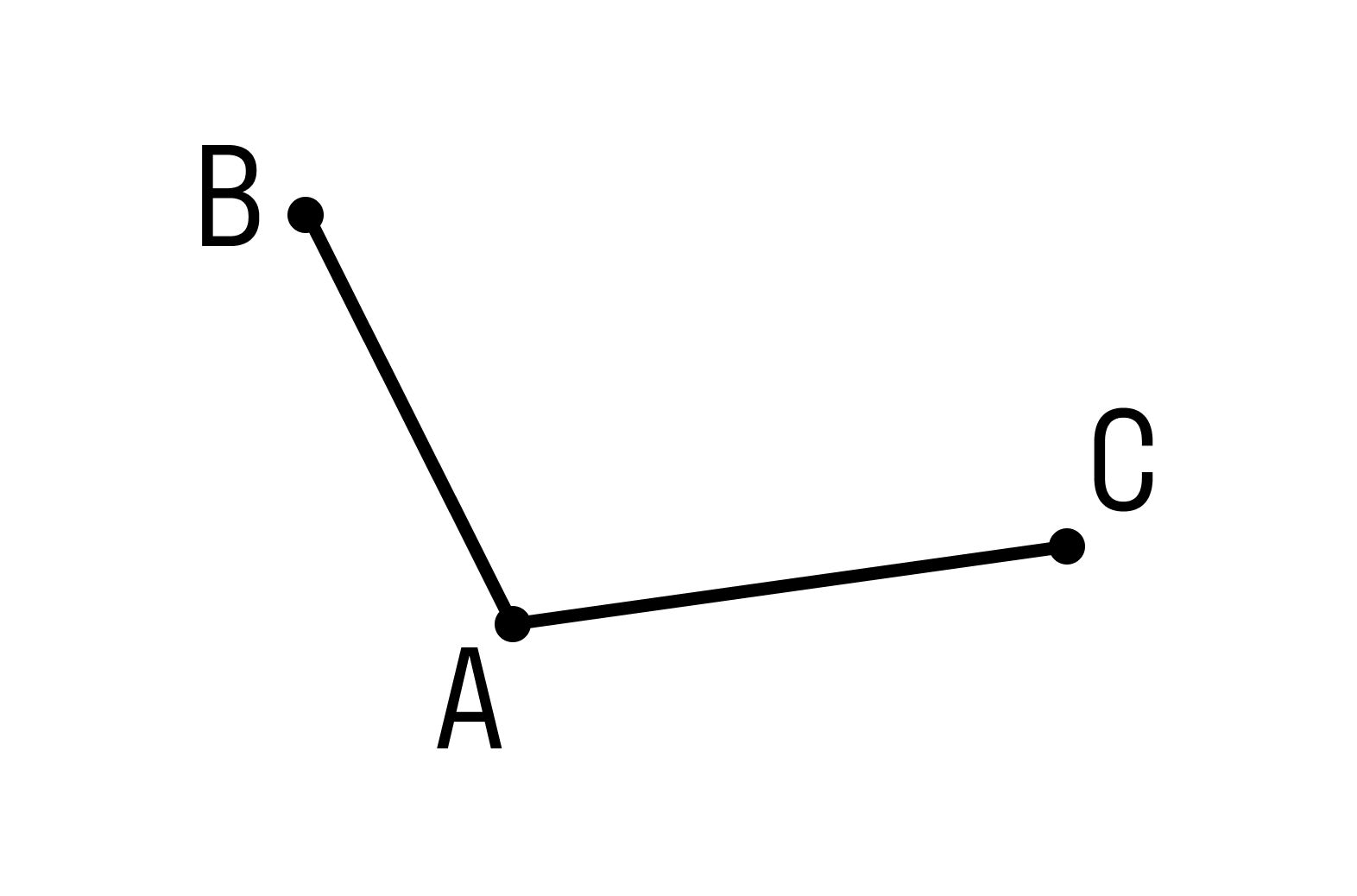
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.

Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.

Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).

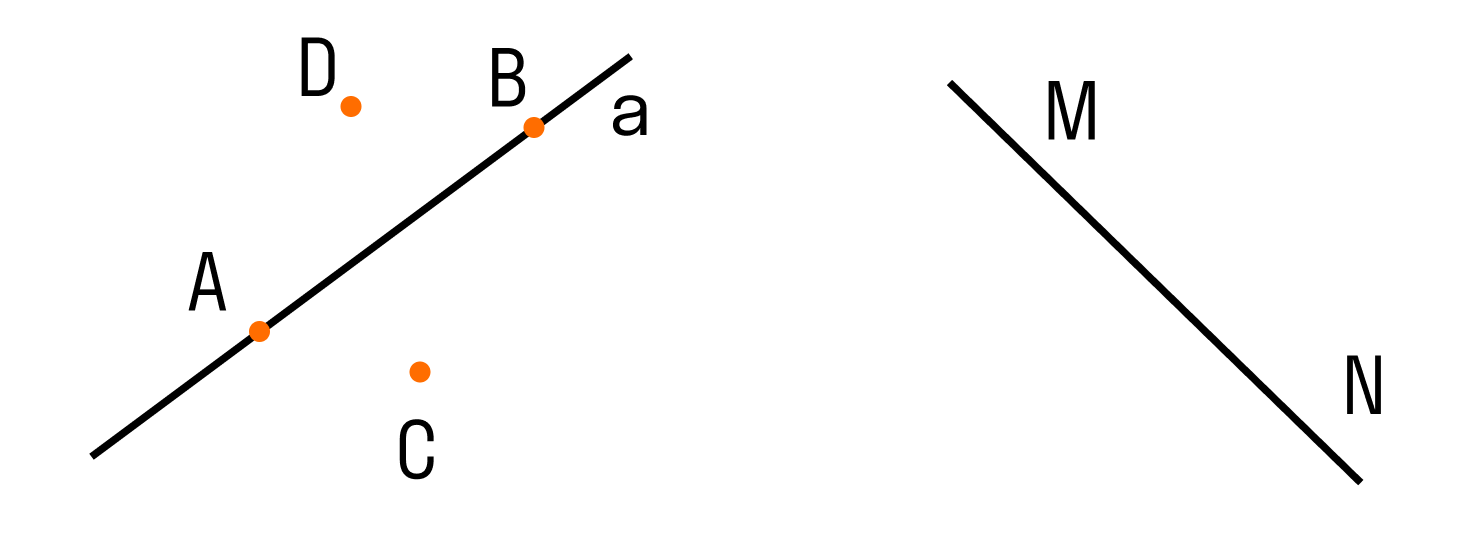
Два варианта расположения точек относительно прямой:

1. Точки лежат на данной прямой. Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).
2. Точки не лежат на данной прямой. Говорят так: прямая не проходит через эти точки — на рисунке такими точками являются С и D. При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).

Важно знать

Через любые две точки можно провести прямую и притом только одну.

Если рассмотреть две прямые, то возможны два варианта их расположения:

1. Прямые пересекаются, то есть имеют одну общую точку.
   Для записи пересекающихся прямых используют специальный знак — ∩ , то есть a ∩ b (читают: прямая a пересекает прямую b).
2. Прямые не пересекаются, то есть не имеют общих точек.
   Для записи не пересекающихся прямых используют специальный знак — ,
   то есть m n (читают: прямая m не пересекает прямую n).

Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.

На рисунке точка О разбивает прямую АВ на две части:

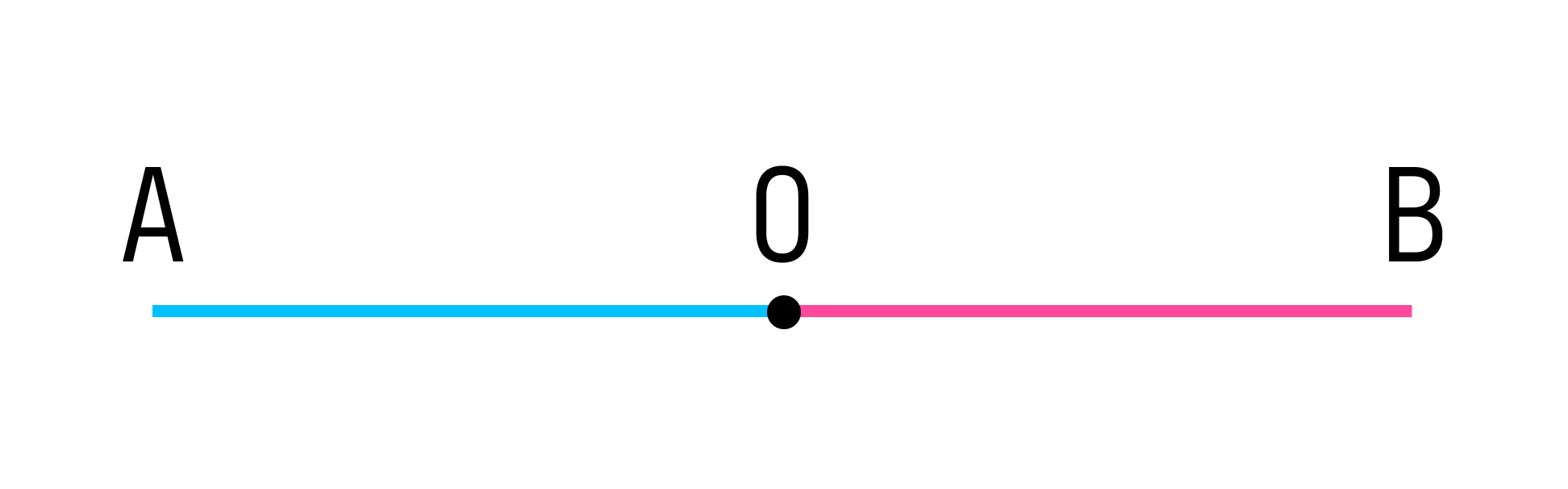
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.

Назовем получившиеся лучи:

• Луч ОА, точка О — начало луча ОА; конца у луча ОА нет.
• Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет.

Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.

Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости

Umath.ru

Веб-сервис Umath.ru — не только набор онлайн-калькуляторов, но и неплохой справочник по математике. Позволяет строить 3 разновидности графиков функций:

• Заданных уравнением.
• Заданных параметрически.
• В полярной системе координат.

В отличие от предыдущего, этот веб-сайт дает возможность размещать несколько графиков на одной плоскости (они будут нарисованы разным цветом). Также он позволяет изменять масштаб и смещать положение центра координатного пространства (кнопки управления находятся слева от графика, но можно пользоваться и мышью).

Готовый результат можно скачать на компьютер в виде картинки.

Достоинства Umath.ru — простота применения (на станице есть пояснения, списки функций и констант), масштабирование, возможность оставлять комментарии, пользоваться справочником и другими математическими калькуляторами. Недостаток — ограниченный функционал (к сожалению, нет возможности строить трехмерные графики) и иногда проскакивающие ошибки. Но, надеемся, это временно, так как сервис активно развивается.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером
в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены —
это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих
стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно
больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250
см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат
(умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 —
это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра
должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали —
проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Длина a
Длина b Расчет
Диагональ c

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же,
не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое
нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из
понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров
не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены
на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Структура учебно-методического комплекса

Лекции В лекциях представлены теоретические основы начертательной геометрии. Содержат текстовую информацию, большое количество иллюстраций, а также интерактивные модели для наглядного представления объектов в трехмерном пространстве. В конце каждой темы лекции расположены задачи по начертательной геометрии для самостоятельного решения для закрепления теоретического материала. 1. Методы проецирования 2. Ортогональные проекции прямой 3. Плоскость 4. Способы преобразования ортогонального чертежа 5. Метод геометрических множеств 6. Многогранники 7. Поверхности 8. Пересечение кривых поверхностей

ПрезентацииПрезентации содержат иллюстративный материал для лекций и в основном предназначены для преподавателей при проведении занятий, а также для студентов, пропустивших лекцию.1. Ортогональные проекции точки2. Ортогональные проекции прямой3. Взаимное положение прямых4. Ортогональные проекции плоскости5. Взаимное положение плоскостей6. Способы преобразования ортогонального чертежа7. Многогранники8. Поверхности

Рабочая тетрадь В рабочей тетради представлены дополнительные задачи по начертательной геометрии, которые полезно прорешать по каждой теме лекции.1. Точка 2. Прямая 3. Плоскость 4. Взаимное положение плоскостей 5. Прямая и плоскость 6. Способы преобразования ортогонального чертежа 7. Пересечение тел прямой и плоскостью 8. Взаимное пересечение поверхностей

Опорный конспектВ опорном конспекте в сжатом графическом виде отражены все основные положения и типовые задачи начертательной геометрии. Методичку удобно использовать для самопроверки и подготовки к экзамену или зачету. Опорный конспект в виде схематических блоков учебной информации (рисунков, алгоритмов) охватывает все основные темы курса и является дополнительным пособием для изучения начертательной геометрии.Тема 1. Методы проецирования. Проекции точки, отрезка прямой Тема 2. Отрезок. Прямая, Взаимное положение прямых. Плоскость Тема 3. Пересечение плоскостей. Пересечение прямой с плоскостью Тема 4. Перпендикуляр к плоскости. Дополнительные плоскости проекций Тема 5. Способ вращения. Многогранники Тема 6. Кривые поверхностиСкачать опорный конспект одним файлом

Контрольные работы Контрольные задания (расчетно-графические работы — РГР) предназначены для домашнего выполнения и сдачи преподавателю. В описании контрольных заданий есть видеоматериалы с пошаговыми действиями решения типовых задач.Задание 1. Построение следов плоскости и определение расстояния от точки до плоскости Задание 2. Построение линии пересечения плоскостей Задание 3. Построение натурального вида сечения пирамиды плоскостью Задание 4. Построение линии пересечения поверхностейЗадание 5. Нахождения истинной формы плоской фигуры способом плоско-параллельного перемещенияЗадание 6. Построение недостающих проекций плоской фигуры, принадлежащей плоскости, заданной следамиЗадание 7. Построение точки пересечения прямой с плоскостью, заданной следамиЗадание 8. Определение расстояния между двумя прямыми способом перемены плоскостей проекций

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных
фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные
или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается
прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить
45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим
два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм
вам понятен.

Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет
вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или
строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.

Оцените публикацию:

• Currently 4.23

Оценка: 4.2 (134 голосов)

Построение вписанного в окружность правильного пятиугольника

Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B. 

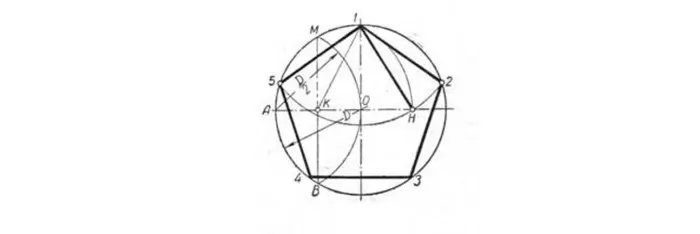
Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника. 

Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.

Задача выполнена.

Onshape позволяет работать с файлами .dwg

Англоязычный онлайн-сервис Onshape предлагает профессиональные решения для проектирования и создания чертежей в системе 3D-cad. К сожалению, бесплатный функционал сайта ограничен 21 днём бесплатного пользования, далее же за возможность создавать чертежи онлайн с помощью Onshape необходимо будет платить «живые» деньги.

Для работы с Onshape перейдите на данный ресурс, нажмите на кнопку «I WANT TO TRY ONSHAPE» (если такой кнопки нет, просто перезагрузите главную страницу сайта).

1. Пройдите расширенную регистрацию для работы с AutoCAD онлайн, и вы окажетесь в окне создания и редактирования чертежей.
2. Для создания нового чертежа нажмите на «Create» (создать), укажите имя документа.
3. Выберите уровень доступа к нему («Private» — личный, «Public» — общедоступный) и нажмите на «Ок».

4. Для сохранения вашего чертежа кликните правой клавишей мыши на закладке вашего файла внизу.

5. Выберите «Export», определитесь с форматом исходящего файла, укажите «Download» и нажмите на «Ок».

Упрощённые сервисы для работы с AutoCAD

Также для осуществления черчения онлайн могут помочь такие сервисы как drawisland.com и sketch.io. Функционал указанных сервисов довольно прост, и может пригодиться, скорее, для развлекательных и бытовых целей, нежели для профессионального черчения.

Рабочее окно сервиса Drawisland

Как начертить многоугольник в AutoCAD описанный вокруг окружности

Многоугольник Автокад описанный вокруг окружности задается центральной точкой и расстоянием от центра до средней точки одной из его сторон. Следовательно, радиус вписанной окружности — это расстояние от центра многоугольника до средней точки одной из его сторон.

Вызываем команду «МН-Угол». Система отобразит запрос:

Число сторон <5 — предыдущее значение>:

Соглашаемся со значением по умолчанию, нажимаем «Enter». Появляется следующий запрос:

Укажите центр многоугольника:

Указываем в Автокад центр многоугольника. Появляется запрос в командной строке:

Задайте параметр размещения [Вписанный в окружность/Описанный вокруг окружности] <В>:

Выбираем опцию «Описанный вокруг окружности» команды МН-Угол. Отобразится предварительный вид многоугольника Автокад, который прикреплен к линии, проходящей из заданного центра до указателя, соответствующего середине одной из сторон многоугольника. Размер многоугольника в Автокад будет изменяться вместе с изменением положения указателя. В командной строке появится запрос:

Радиус окружности:

Повторим ввод координат и зададим радиус описанной окружности с помощью задания относительных полярных координат. Введем в командную строку следующее значение @20<0, что означает:

• «@» — отсчет координат ведется от центральной точки многоугольника Автокад;
• «20» — расстояние от центральной точки, т.е. радиус вписанной окружности;
• «<» обозначение полярности координат — возможности привязки к определенному углу;
• «0» — значение угла, т.е. 0 градусов.

Правильный многоугольник в Автокад с радиусом вписанной окружности 20 мм построен.

Совет
Задав радиус вписанной или описанной окружности в командной строке путем ввода значения радиуса, многоугольник в Автокад автоматически выравнивается так, чтобы его нижняя сторона располагалась параллельно оси X текущей ПСК. Если задать радиус при помощи мыши (различными методами задания координат), то можно повернуть многоугольник вокруг центра на нужный угол.

Desmos

Портал Desmos.com, в отличие от многих других, может хранить ваши графики в своей базе и позволяет делиться с другими юзерами ссылками на них. Однако для этого придется зарегистрироваться на ресурсе.

Поддерживает построение следующих видов графиков:

• постоянных функций (например, y=x+2);
• зависимости x от y (x=√(2-y));
• неравенств (x≤2-y);
• кусочно-заданных функций (y={x<0: -x, x});
• в полярных координатах (r(t)=sin(6t));
• по точке и группе точек ((1,2), (2,3), (3,4));
• движения точки;
• функций с параметром (y = |x2 – 2x – 1|);
• сложных функций (y = ln cos x).

Также он может конвертировать введенные пользователем выражения в таблицы.

Интерфейс Desmos.com несколько отличается от аналогов. Большую часть окна занимает настраиваемая координатная плоскость. В ней можно включать и выключать видимость осей, изменять вид и величину шага сетки, переключаться между градусами и радианами, а также — менять масштаб плоскости и смещать центральную точку.

Слева находится скрываемая панель ввода выражений. Над ней — кнопка «гамбургер», щелчком по которой открывается список примеров различных чертежей. Рядом с кнопкой отображается имя текущего графика, но в нашем случае его нет, так как опция доступна только зарегистрированным пользователям.

Внизу окна — скрываемая виртуальная клавиатура.

Для демонстрации графиков аудитории на Desmos.com предусмотрен режим проектора (кнопка его включения скрыта в настройках координатной плоскости за иконкой гаечного ключа). В этом режиме все линии становятся толще, а надписи -крупнее.

Мы привели лишь краткое описание функциональности сервиса. Если вам нужна справка по работе с ним на русском языке, она находится здесь.

Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.